A to Z of Excel Functions: The ERF Function

Welcome back to our regular A to Z of Excel Functions blog. Today we look at the ERF function.

The ERF function

In mathematics, the error function (also called the Gauss error function or ERF) is a special, non-elementary function that occurs in probability, statistics and partial differential equations describing diffusion. It is defined as:

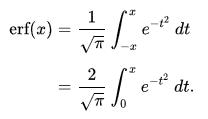
In statistics, for nonnegative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and variance 1/2, ERF(x) describes the probability of Y falling in the range [?x, x].

This function returns the error function integrated between lower_limit and upper_limit.

The ERF function employs the following syntax to operate:

The ERF function has the following arguments:

• lower_limit: this is required and represents the lower bound for integrating ERF
• upper_limit: this argument is optional. This represents the upper bound for integrating ERF. If omitted, ERF integrates between zero and lower_limit.

It should be further noted that:

• if lower_limit is nonnumeric, ERF returns the #VALUE! error value
• if upper_limit is nonnumeric, ERF returns the #VALUE! error value.

Please see my example below:

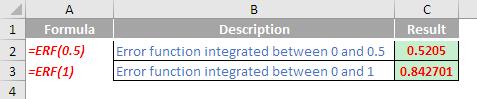
We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every business day.

A full page of the function articles can be found here.