Power Pivot Principles: The A to Z of DAX Functions – COTH

In our long-established Power Pivot Principles articles, we continue our series on the A to Z of Data Analysis eXpression (DAX) functions.  This week, we look at COTH.

The COTH function

This function returns the hyperbolic cotangent of a hyperbolic angle.  Clear as mud?  Just as the points (cos t, sin t) form a circle with a unit radius, the points (cosh z, sinh z) form the right half of the equilateral hyperbola.  The hyperbolic functions take a real argument called a hyperbolic angle.  The size of a hyperbolic angle is twice the area of its hyperbolic sector.  The hyperbolic functions may be defined in terms of the legs of a right triangle covering this sector.

Hyperbolic functions occur in the solutions of many linear differential equations, such as some cubic equations.  Further, in complex analysis, the hyperbolic functions arise as the imaginary parts of sine and cosine – but that’s a story for another day.

Essentially, COTH(N) is equal to COSH(N) divided by SINH(N).  The COTH function employs the following syntax to operate:

The COTH function has the following arguments:

• number: this is required.

It should be further noted that:

• the hyperbolic cotangent is analogous to the ordinary (circular) cotangent
• the absolute value of number must be less than 2^27 and cannot be zero [0]
• if number exceeds its constraints, an error is returned
• if number is a non-numeric value, an error is returned.

The following equation is used:

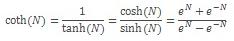
This function is not supported for use in DirectQuery mode when used in calculated columns or row-level security (RLS) rules.

Please see my example below: 

Come back next week for our next post on Power Pivot in the Blog section.  In the meantime, please remember we have training in Power Pivot which you can find out more about here.  If you wish to catch up on past articles in the meantime, you can find all of our Past Power Pivot blogs here.